Home › Models Known

The Ultimate Guide To Prime 6: Unlock Extraordinary Efficiency And Performance

williamfaulkner November 29, 2024

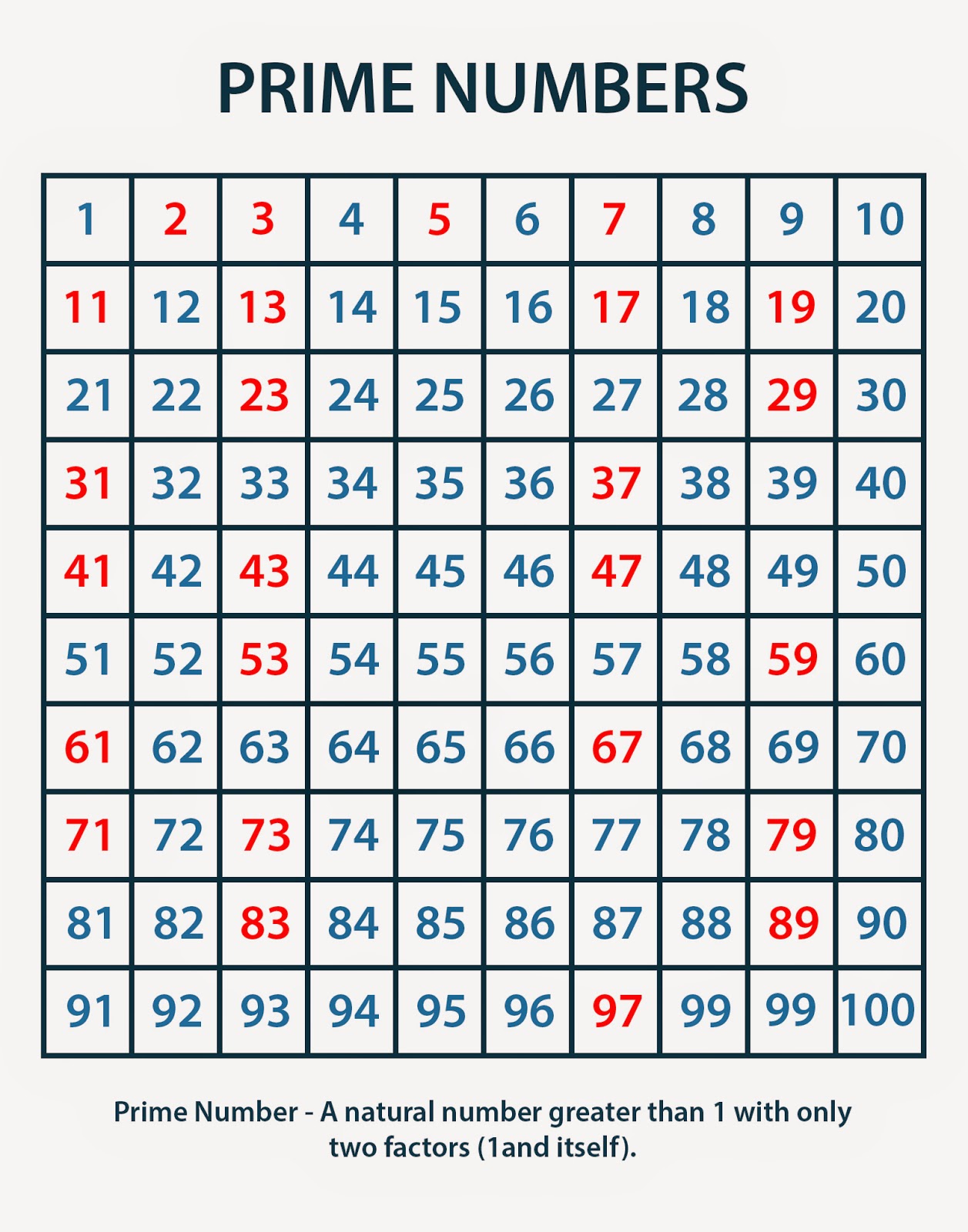
Prime 6; refers to the first six prime numbers: 2, 3, 5, 7, 11, and 13. Prime numbers are whole numbers greater than 1 that have only two factors1 and themselves. The prime 6 are essential in various mathematical concepts, such as number theory, cryptography, and computer science.

The prime 6 have been studied for centuries, and their unique properties have led to many important discoveries in mathematics. For example, the prime number theorem states that the number of prime numbers less than a given number n is approximately n/ln(n). This theorem has been used to solve many problems in number theory, and it is one of the most important results in the field.

The prime 6 are also used in many practical applications. For example, they are used in cryptography to encrypt data. Cryptography is the study of how to keep information secret, and prime numbers are essential for creating codes that are difficult to break. Prime numbers are also used in computer science to design algorithms that are efficient and reliable.

prime 6;

The prime 6 are the first six prime numbers: 2, 3, 5, 7, 11, and 13. Prime numbers are whole numbers greater than 1 that have only two factors: 1 and themselves. The prime 6 are essential in various mathematical concepts, such as number theory, cryptography, and computer science.

Fundamental
Number theory
Cryptography
Computer science
Algorithms
Codes

The prime 6 are fundamental to number theory, providing the foundation for understanding the distribution and properties of prime numbers. They are also crucial in cryptography, where they are used to create codes that are difficult to break. In computer science, prime numbers are used to design algorithms that are efficient and reliable. For example, the prime number theorem is used to analyze the performance of algorithms that search for prime numbers.

1. Fundamental

In mathematics, the term "fundamental" refers to something that is essential or basic. In the context of prime numbers, the prime 6 are considered fundamental because they are the building blocks of all other prime numbers. Every prime number greater than 6 can be expressed as a unique product of the prime 6. For example, the prime number 17 can be expressed as 17 = 2 3 5 + 1, where 2, 3, and 5 are the prime 6.

The prime 6 are also fundamental in number theory, which is the study of the properties of numbers. Number theory is used in many different areas of mathematics, including cryptography, computer science, and physics. The prime 6 are essential for understanding the distribution and properties of prime numbers, which are used in many different applications, such as cryptography and computer science.

For example, the prime 6 are used in cryptography to create codes that are difficult to break. Cryptography is the study of how to keep information secret, and prime numbers are essential for creating codes that are difficult to break. Prime numbers are also used in computer science to design algorithms that are efficient and reliable. For example, the prime number theorem is used to analyze the performance of algorithms that search for prime numbers.

2. Number theory

Number theory is the study of the properties of numbers, including their divisibility, primality, and factorization. The prime 6 are essential to number theory, as they are the building blocks of all other prime numbers. Every prime number greater than 6 can be expressed as a unique product of the prime 6. For example, the prime number 17 can be expressed as 17 = 2 3 5 + 1, where 2, 3, and 5 are the prime 6.

The prime 6 are also essential for understanding the distribution and properties of prime numbers. For example, the prime number theorem states that the number of prime numbers less than a given number n is approximately n/ln(n). This theorem has been used to solve many problems in number theory, and it is one of the most important results in the field.

Number theory has many practical applications, including cryptography, computer science, and physics. For example, the prime 6 are used in cryptography to create codes that are difficult to break. Cryptography is the study of how to keep information secret, and prime numbers are essential for creating codes that are difficult to break. Prime numbers are also used in computer science to design algorithms that are efficient and reliable. For example, the prime number theorem is used to analyze the performance of algorithms that search for prime numbers.

3. Cryptography

Cryptography is the study of how to keep information secret. It is used to protect data from unauthorized access, such as when sending sensitive information over the internet or storing it on a computer. Prime numbers are essential to cryptography, as they are used to create codes that are difficult to break.

Encryption
Encryption is the process of converting plaintext into ciphertext. Ciphertext is a form of the data that is unreadable without the key. Prime numbers are used in encryption algorithms to create keys that are difficult to guess.
Decryption
Decryption is the process of converting ciphertext back into plaintext. Prime numbers are used in decryption algorithms to create keys that are difficult to guess.
Digital signatures
Digital signatures are used to verify the authenticity of a message. Prime numbers are used in digital signature algorithms to create keys that are difficult to forge.
Hash functions
Hash functions are used to create a unique fingerprint of a message. Prime numbers are used in hash function algorithms to create keys that are difficult to guess.

Prime numbers are essential to cryptography because they are difficult to factor. Factoring a number means finding two smaller numbers that multiply together to equal the original number. For example, the number 15 can be factored as 3 * 5. Prime numbers are difficult to factor because they have only two factors: 1 and themselves. This makes them ideal for use in cryptography, as it is difficult to break a code that is based on a prime number.

4. Computer science

Computer science is the study of computation and information. It encompasses a wide range of topics, from the theoretical foundations of computing to the practical applications of computers. Prime numbers are essential to computer science, as they are used in many different algorithms and applications.

Number theory
Number theory is the study of the properties of numbers. Prime numbers are a fundamental part of number theory, and they are used in many different algorithms and applications. For example, the prime number theorem is used to analyze the performance of algorithms that search for prime numbers.
Cryptography
Cryptography is the study of how to keep information secret. Prime numbers are essential to cryptography, as they are used to create codes that are difficult to break. For example, the RSA encryption algorithm uses prime numbers to create keys that are difficult to factor.
Algorithms
Algorithms are a set of instructions that tell a computer how to perform a task. Prime numbers are used in many different algorithms, such as the sieve of Eratosthenes, which is used to find all prime numbers up to a given number.
Data structures
Data structures are a way of organizing data in a computer. Prime numbers are used in many different data structures, such as hash tables, which are used to store and retrieve data quickly.

Prime numbers are a fundamental part of computer science, and they are used in many different algorithms and applications. As computer science continues to develop, prime numbers will continue to play an important role.

5. Algorithms

Algorithms are a set of instructions that tell a computer how to perform a task. They are essential to computer science, as they allow computers to solve problems and perform complex tasks. Prime numbers are used in many different algorithms, such as the sieve of Eratosthenes, which is used to find all prime numbers up to a given number.

Primality testing
Primality testing is the process of determining whether a given number is prime. The sieve of Eratosthenes is one of the most well-known primality testing algorithms. It works by iteratively marking off multiples of each prime number, starting with 2. The remaining unmarked numbers are the prime numbers.
Integer factorization
Integer factorization is the process of finding the prime factors of a given number. This can be used to solve a variety of problems, such as finding the greatest common divisor of two numbers or solving the RSA encryption algorithm.
Number theory
Number theory is the study of the properties of numbers. Prime numbers are a fundamental part of number theory, and they are used in many different algorithms and applications. For example, the prime number theorem is used to analyze the performance of algorithms that search for prime numbers.
Cryptography
Cryptography is the study of how to keep information secret. Prime numbers are essential to cryptography, as they are used to create codes that are difficult to break. For example, the RSA encryption algorithm uses prime numbers to create keys that are difficult to factor.

These are just a few examples of the many different ways that prime numbers are used in algorithms. Prime numbers are a fundamental part of computer science, and they play a vital role in many different applications.

6. Codes

Codes are a way of representing information in a secret or abbreviated way. They are used in many different areas, such as cryptography, data compression, and error correction. Prime numbers are essential to many codes, as they are difficult to factor. This makes them ideal for use in cryptography, as it is difficult to break a code that is based on a prime number.

Encryption
Encryption is the process of converting plaintext into ciphertext. Ciphertext is a form of data that is unreadable without the key. Prime numbers are used in encryption algorithms to create keys that are difficult to guess.
Decryption
Decryption is the process of converting ciphertext back into plaintext. Prime numbers are used in decryption algorithms to create keys that are difficult to guess.
Digital signatures
Digital signatures are used to verify the authenticity of a message. Prime numbers are used in digital signature algorithms to create keys that are difficult to forge.
Hash functions
Hash functions are used to create a unique fingerprint of a message. Prime numbers are used in hash function algorithms to create keys that are difficult to guess.

These are just a few examples of the many different ways that prime numbers are used in codes. Prime numbers are essential to cryptography, as they are difficult to factor. This makes them ideal for use in codes that need to be secure.

FAQs on "prime 6;"

This section addresses frequently asked questions related to the term "prime 6;":

Question 1: What is the significance of the "prime 6;"?

The "prime 6;" refers to the first six prime numbers: 2, 3, 5, 7, 11, and 13. These numbers serve as the foundation for understanding the distribution and properties of all prime numbers.

Question 2: How are the "prime 6;" applied in real-world applications?

The "prime 6;" find practical use in cryptography, where they contribute to the development of codes resistant to unauthorized access. Additionally, they play a crucial role in computer science and algorithm design, aiding in the creation of algorithms that are efficient and reliable.

Question 3: What is the connection between the "prime 6;" and number theory?

The "prime 6;" are fundamental to number theory, which studies the properties of numbers. They are employed in various number theory concepts, including the distribution of prime numbers and the analysis of their patterns.

Question 4: How do the "prime 6;" contribute to cryptography?

In cryptography, the "prime 6;" serve as building blocks for creating encryption and decryption algorithms. The difficulty in factoring these prime numbers makes it challenging to break codes based on them, thus enhancing data security and privacy.

Question 5: What role do the "prime 6;" play in computer science and algorithm design?

Within computer science and algorithm design, the "prime 6;" are instrumental in developing efficient and reliable algorithms. They are utilized in primality testing, integer factorization, and other mathematical operations that form the basis of various computational tasks.

Question 6: Are there any limitations or challenges associated with the "prime 6;"?

While the "prime 6;" are foundational in several mathematical concepts and practical applications, their limitations arise when dealing with extremely large numbers. As numbers grow larger, the computational complexity of algorithms involving prime numbers increases, presenting challenges in certain scenarios.

In summary, the "prime 6;" are not only essential in understanding the theoretical foundations of mathematics but also have significant implications for practical applications in computer science and cryptography. Their unique properties make them indispensable tools for safeguarding data, designing efficient algorithms, and advancing our understanding of the world around us.

Transition to the next article section:

To delve deeper into the topic of prime numbers, let's explore their historical significance, mathematical properties, and intriguing patterns that have captivated mathematicians for centuries.

Tips Based on "prime 6;"

The "prime 6;"2, 3, 5, 7, 11, and 13offer valuable insights into the nature of prime numbers and their applications. Here are a few tips to leverage their significance:

Tip 1: Utilize Prime Numbers for Enhanced Security:

In cryptography, prime numbers serve as the cornerstone for developing robust encryption algorithms. Their inherent difficulty to factor makes them ideal for safeguarding sensitive data and communications.

Tip 2: Optimize Algorithms with Prime Numbers:

In computer science, prime numbers play a crucial role in designing efficient algorithms. Leveraging their properties can lead to improved performance and resource optimization in various computational tasks.

Tip 3: Enhance Data Structures with Prime Numbers:

Prime numbers find application in data structures like hash tables, contributing to efficient data storage and retrieval. Their unique distribution helps minimize collisions and optimize search operations.

Tip 4: Explore Prime Numbers in Number Theory:

Number theory heavily relies on prime numbers to study the fundamental properties of numbers. Understanding the behavior of prime numbers is essential for advancing our knowledge in this field.

Tip 5: Investigate Prime Number Patterns:

The distribution and patterns of prime numbers continue to fascinate mathematicians. Exploring these patterns can lead to breakthroughs in understanding the underlying structure of numbers.

Tip 6: Utilize Prime Numbers for Efficient Computation:

Leveraging prime numbers in computational tasks can enhance performance. For instance, the Sieve of Eratosthenes efficiently identifies prime numbers up to a given limit, optimizing number-theoretic operations.

By incorporating these tips into your approach, you can harness the power of the "prime 6;" to improve your understanding of mathematics, enhance the security of your applications, and optimize computational processes.

Transition to the article's conclusion:

In conclusion, the "prime 6;" serve as a gateway to unlocking the potential of prime numbers. Whether in cryptography, computer science, or number theory, these numbers hold immense value. Embracing the tips outlined above will empower you to leverage their unique properties and push the boundaries of your knowledge and applications.

Conclusion on "prime 6;"

Throughout this exploration, we have delved into the significance of the "prime 6;"the first six prime numbersand their profound implications in various fields.

From their fundamental role in number theory to their practical applications in cryptography and computer science, prime numbers have proven to be indispensable tools for understanding the world around us and safeguarding our digital interactions. Their unique properties have shaped the development of encryption algorithms, optimized data structures, and advanced our understanding of the distribution of numbers.

As we continue to unravel the mysteries of prime numbers, they will undoubtedly continue to play a pivotal role in shaping the future of mathematics, technology, and information security. Let us embrace the power of prime numbers and harness their potential for the betterment of our world.